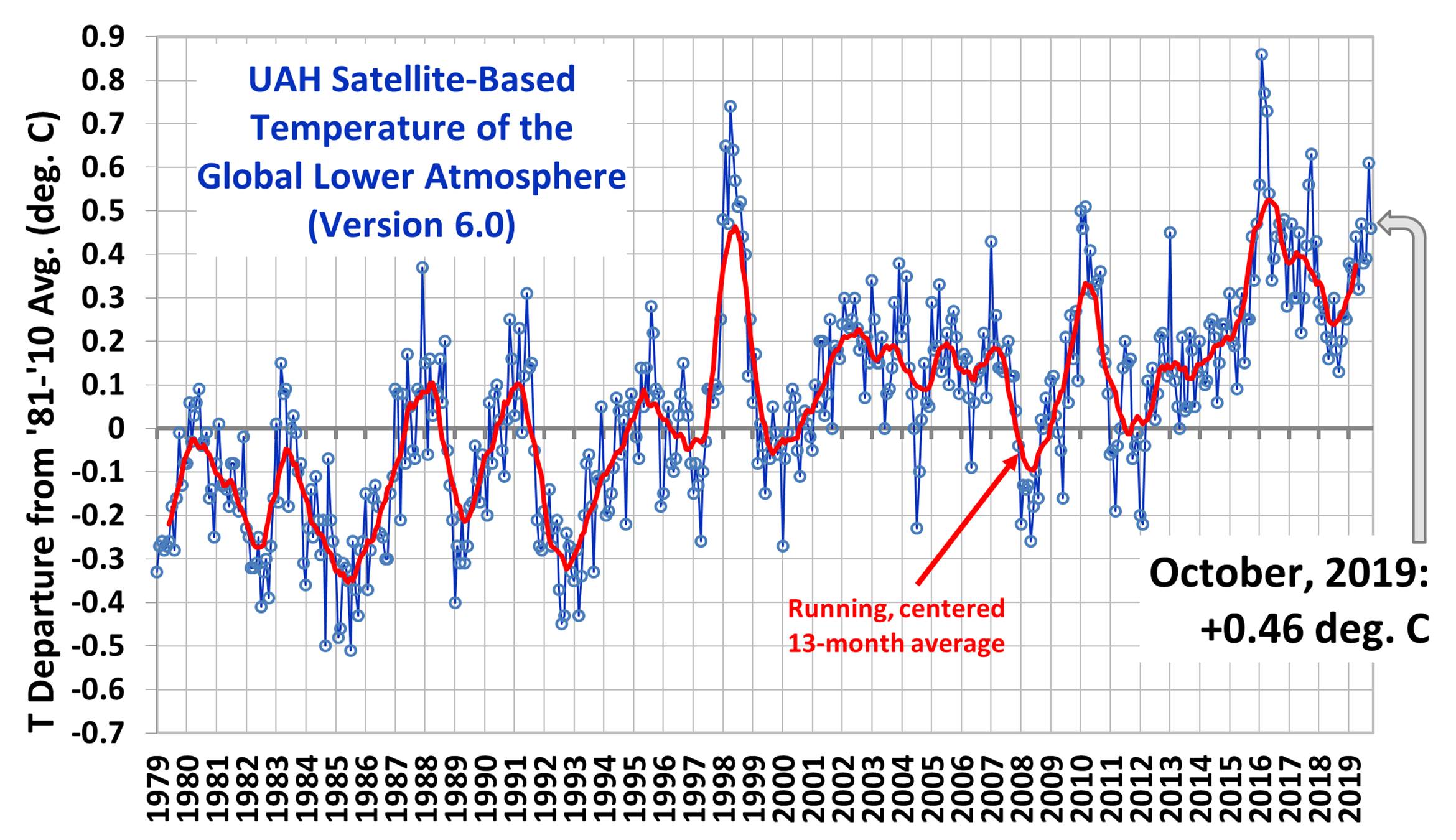
I'm sure there are some real statistics experts here, so could someone please explain, how is that green line a median for the graph in post number 25?
Also
Isn't it statistically really strange for the average depicted in the graph on the article posted in #3, to so closely reflect the median?
To help explain my question, it is my understanding that the median is the point right in the middle of the data range, not the mean or the modal point. Maybe I'm misunderstanding the data, but they don't seem like a good representation. As was pointed out, to even talk about the standard deviation, the data set has to be normalized, a symmetrical bell curve, otherwise, there are multiple possible s.d.s for the each side of the average.
-Will (Dragonfly)
The mean (arithmetic average), mode and median are the three measures of central tendency. Each have their own strengths and weaknesses. The purpose of a measure of central tendency is to provide one number that best reflects the distribution. That's how airline seats are designed, what size bottom will cause the least distress to the largest number of passengers.
In a normal distribution of infinite size the mean, mode and median are the same. However, in the real world we are often dealing with fewer than infinite elements in a distribution, thus the three may not be equal.
Because the average is an arithmetically derived number, it can be used in other calculations, such as calculating standard deviations and various statistical analyses (t-Test, ANOVA, ANACOVA, etc.). A drawback to an arithmetical average is its sensitivity to magnitude of the differences in the values in the data set, especially small data sets. Consider 3 teachers sitting in a bar talking about salary, the first one says he makes $50K, the next $60K and the third $70K. In this case the mean is $60K and the median is $60K. (Because there are only 3 unique values, the mode really doesn't tell us much, the distribution has 3 modes, I.e., each individual element.)
The median is the midpoint in the data range, half the values are higher than the median half are lower. The median may not be equal to any element in the data set. The median of 2, 3, 5, 6 is 4. The strength of the median is the lack of sensitivity to the magnitude of the differences between elements, the median for the distribution of 2, 3, 5, 1K is 4. The median is an ordinal number, because it is ordinal it can not be used in a mathematical calculation, it is simply description. Ordinal numbers simply identify the data point position in the distribution. The median is the middle position when the data points are arranged from lowest to highest.
Modes simply identify the most frequently occurring value. They are helpful in describing a distribution but aren't used for much. If the mode is about the same as the mean and median, then the distribution is more likely to be a normal distribution (bell curve or Gaussian distribution).
Now lets get back to the bar with our three teachers. Another person sits down at the table and orders a beer. Turns out he's a retail clerk at a big box marine store and he's complaining about his salary which turns out to be a measly $30K. The median salary for bar patrons is now 55K as that is the midpoint, 30K, 50K, (55K), 60K, 70K. Remember, the median does not have to be an element of the data set. The mean is now $52.5 K. In this case the median only dropped 5K while the mean dropped 7.5K.
A little while later a fifth person sits down at the table and orders a bottle of Dom Perignon. We know right away this person is not a teacher nor a WM employee. As introductions are made, it turns out he's a retired tech guy who goes by the name of Bill. (Except in certain circles in Cupertino, CA.) The conversation returns to salaries and Bill mentions he had a good year with his income reaching 10 or 11 digits.
The salary distribution now looks like this: 30K, 50K, 60K, 70K, 1 bazillion. What's the median? It goes back to $60K, that is the midpoint in the distribution. The mean however is now something like .20 bazillion, considerably more than 60K. Going back to the purpose of a measure of central tendency which better describes our group of bar patrons? The mean of .20 bazillion or the median of 60K? Obviously the answer is the median, more of our patrons are earning close to 60K than to .20 bazillion.
Back to the green line in #25. The median line is flat and given the values in the graph this is the appropriate measure because it is insensitive to wild swings. One of the reasons statistics developed was to predict farm yields. With weather meteorologists and climatologists are trying to predict future weather. The flat median line says, past ice coverage does not predict future ice coverage. That is, in any given year it is equally likely that there will more or less ice than average. It doesn't do anything to explain why or how much difference there will be.
Consider another scenario where the median is trending downward (to less ice coverage). In this scenario the safe bet would be to predict less ice coverage in the next year, because the trend has been towards less ice coverage.
The interesting aspect of the graph is not the median line, it is the wide variation from year to year. That variation would be measured by a standard deviation. Large standard deviations indicate that the data is distributed across a wide range, a small deviation suggests the distribution is narrow. When the SD of a distribution is narrow or small, predictions can be made more accurately than if the distribution is large. For example if the range is from 1 to 10, there is a 10% chance of making the right prediction; if the range is 1 to 100 the chance declines to 1%. Returning the graph, in the first 5 years the range is roughly 12% to 36% coverage. In the years from 2012 to 2017 the range is much different, 3% to 37%.
So that's the simple basic version and it is atheortetical and does not attempt to factor in any other climate or weather data. The next levels of analysis involve adding multiple factors into regression equations that attempt to add increased descriptive and predictive accuracy. And when I consider those ideas, I get flashbacks to PSY 896 and orthogonal rotations in multidimensional spaces and blackboards covered in matrices.
Does this help?